In this Masterclass, we will discuss how to monitor and optimize the performances of a PLUMED-enhanced MD simulation.
Once you have completed this Masterclass you will be able to:
For this masterclass you will need versions of PLUMED and GROMACS that are compiled using the MPI library. Thus follow the instructions that are reported for PLUMED Masterclass 21.5: Simulations with multiple replicas.
Natively-compiled GROMACS and PLUMED will be significantly faster than the conda versions that we are providing. Since we are focusing on performance here, this might be the right time to learn how to install them on your own.
The data needed to execute the exercises of this Masterclass can be found on GitHub. You can clone this repository locally on your machine using the following command:
git clone https://github.com/plumed/masterclass-21-7.git
Notice that the results of these exercises might depend on the details of the hardware and software you are using. It is thus instructive to test them on different architectures, or with different PLUMED or GROMACS versions.
In these exercises you will have to maximise the performance of your simulation. When using GROMACS, the common way to report performances is to check at how many ns/day the simulation can produce. At the end of the log file you should find lines like these ones
Core t (s) Wall t (s) (%)
Time: 141.898 11.825 1200.0
(ns/day) (hour/ns)
Performance: 14.628 1.641
Here, the higher the ns/day the faster your simulation will be. Another important information it the wallclock time, that indicates how many seconds elapsed since the start of your simulation. If you then run the same input file using PLUMED as well you will instead see something like this:
Core t (s) Wall t (s) (%)
Time: 170.519 14.210 1200.0
(ns/day) (hour/ns)
Performance: 12.173 1.972
Finished mdrun on rank 0 Thu Apr 22 16:37:32 2021
PLUMED: Cycles Total Average Minimum Maximum
PLUMED: 1 2.009397 2.009397 2.009397 2.009397
PLUMED: 1 Prepare dependencies 1001 0.004042 0.000004 0.000003 0.000013
PLUMED: 2 Sharing data 1001 0.151432 0.000151 0.000032 0.019904
PLUMED: 3 Waiting for data 1001 0.021681 0.000022 0.000005 0.013026
PLUMED: 4 Calculating (forward loop) 1001 1.392920 0.001392 0.000349 0.032230
PLUMED: 5 Applying (backward loop) 1001 0.303819 0.000304 0.000089 0.025517
PLUMED: 6 Update 1001 0.003255 0.000003 0.000002 0.000175
Notice that:
Notice that the total time spent using PLUMED is approximately equal to the increment in the wallclock time. This might be different when using a GPU (and indeed the increment in the wallclock time should be smaller). This extra time measures the cost of using PLUMED. The goal of this Masterclass is to understand how to decrease this extra time without impacting the result of your simulation.
Notice that PLUMED gives a breakdown of the time spent. Some rows correspond to communication, and might become important if you run with a lot of MPI processes. Usually, most of the time is spent in the forward loop, where collective variables are calculated.
You can obtain a more detailed breakdown adding to your input this line:

DEBUGDETAILED_TIMERS( default=off ) switch on detailed timers
The tail of the log will then look like this:
PLUMED: Cycles Total Average Minimum Maximum PLUMED: 1 2.055374 2.055374 2.055374 2.055374 PLUMED: 1 Prepare dependencies 1001 0.004168 0.000004 0.000003 0.000023 PLUMED: 2 Sharing data 1001 0.118547 0.000118 0.000033 0.016011 PLUMED: 3 Waiting for data 1001 0.008541 0.000009 0.000005 0.000035 PLUMED: 4 Calculating (forward loop) 1001 1.449592 0.001448 0.000375 0.034236 PLUMED: 4A 0 @0 1001 0.004118 0.000004 0.000002 0.000134 PLUMED: 4A 4 d 1001 0.293253 0.000293 0.000011 0.023584 PLUMED: 4A 5 cn 1001 0.810816 0.000810 0.000308 0.034087 PLUMED: 4A 7 @7 11 0.000045 0.000004 0.000003 0.000008 PLUMED: 4A 8 @8 1001 0.225797 0.000226 0.000016 0.021056 PLUMED: 4A 9 @9 1001 0.066718 0.000067 0.000010 0.016033 PLUMED: 5 Applying (backward loop) 1001 0.349111 0.000349 0.000120 0.025091 PLUMED: 5A 0 @9 1001 0.003697 0.000004 0.000003 0.000015 PLUMED: 5A 1 @8 1001 0.002814 0.000003 0.000002 0.000012 PLUMED: 5A 2 @7 11 0.000023 0.000002 0.000002 0.000002 PLUMED: 5A 4 cn 1001 0.102383 0.000102 0.000063 0.013438 PLUMED: 5A 5 d 1001 0.008055 0.000008 0.000006 0.000148 PLUMED: 5A 9 @0 1001 0.002417 0.000002 0.000002 0.000014 PLUMED: 5B Update forces 1001 0.191250 0.000191 0.000020 0.023919 PLUMED: 6 Update 1001 0.003271 0.000003 0.000002 0.000166
Notice that for both the forward and the backward loop you are shown with a breakdown of the time required for each of the actions included in the input file. You should recognize the name of the actions that you defined, whereas unnamed actions are referred to with a generic @-number that corresponds to their position in the input file. From this detailed log you can also appreciate how often each action has been performed. PLUMED tries to optimize this, e.g., only computing variables when they are needed. This breakdown is very useful to know where you should direct your effort.
As a first test system we will consider a single Na Cl pair in a water box. The two ions are expected to attract each other, so that the bound conformation should be stable. The free energy as a function of the distance between the two ions should thus have a minimum followed by a barrier. At larger distances, it is not expected to become flat but rather to decrease as -2*kBT log d, due to the entropic contribution, and then to grow again when reaching the boundaries of the simulation box. In this exercise we will compute the free-energy as a function of the distance between the two ions. As collective variables we will use the distance between the two ions as well as the number of water oxygens that are coordinated with the sodium ion.
In the data/exercise1 folder of the GitHub repository of this Masterclass, you will find a topol.tpr file, which is needed to perform a MD simulation of this system with GROMACS. You can then create a plumed.dat file like this one as a starting point:

# vim:ft=plumed NA: GROUPATOMS=1 CL: GROUPthe numerical indexes for the set of atoms in the group.ATOMS=2 WAT: GROUPthe numerical indexes for the set of atoms in the group.ATOMS=3-8544:3 d: DISTANCEthe numerical indexes for the set of atoms in the group.ATOMS=NA,CL cn: COORDINATIONthe pair of atom that we are calculating the distance between.GROUPA=1First list of atoms.GROUPB=WATSecond list of atoms (if empty, N*(N-1)/2 pairs in GROUPA are counted).R_0=0.3 PRINTcould not find this keywordARG=d,cnthe input for this action is the scalar output from one or more other actions.STRIDE=100compulsory keyword ( default=1 ) the frequency with which the quantities of interest should be outputFILE=COLVAR METADthe name of the file on which to output these quantitiesARG=d,cnthe input for this action is the scalar output from one or more other actions.SIGMA=0.05,0.1compulsory keyword the widths of the Gaussian hillsHEIGHT=0.1the heights of the Gaussian hills.PACE=10compulsory keyword the frequency for hill additionBIASFACTOR=5use well tempered metadynamics and use this bias factor.
As usual, you can run a simulation with the following command
gmx_mpi mdrun -plumed plumed.dat -nsteps 100000
For the first three points, you can run relatively short simulations, so choose nsteps based on what you can quickly test on your machine. For the fourth point instead you will need to reach convergence. A time on the order of a ns should be more the sufficient.
For this first point, we will focus on the calculation and update of the metadynamics bias. We will try to have a simulation that runs faster without changing significantly the result. Check the manual of METAD and find out how to speed up this calculation. A few hints:
Notice that these changes are not expected to impact the convergence of the algorithm. Thus, you do not need a converged simulation to measure the impact on performances.
For this second point, we will focus on the calculation of one of the two biased collective variables, namely the coordination of the Na ion with water oxygens. We will try to have a simulation that runs faster without changing significantly the result. Check the manual of COORDINATION and find out how to speed up this calculation. A few hints:
Notice that these changes are not expected to impact the convergence of the algorithm. Thus, you do not need a converged simulation to measure the impact on performances.
For this third point, we will try to make sure that GROMACS runs at its maximum speed. For this you will have to check GROMACS manual. A few hints:
-pin on option improves performances.Notice that these changes are not expected to impact the convergence of the algorithm. Thus, you do not need a converged simulation to measure the impact on performances.
We will now make modifications to the algorithm so as to be able to arrive to the same result running a shorter simulation. Try to play with METAD parameters and see if you can improve them. A few hints:
Notice that these changes are expected to impact the convergence of the algorithm. Thus, you do not need a converged simulation to measure the impact on performances, and you have to make sure that the statistical accuracy is comparable.
As a final step, analyze the simulations performed so far to compute the standard binding free energy between the two species. Notice that even though this is defined at 1M concentration, the calculations that you are running are actually at infinite dilution.
In this exercise, we will work with the C-terminal domain (CTD) of the RfaH virulence factor from Escherichia coli introduced in PLUMED Masterclass 21.4: Metadynamics (see Exercise 6: A 'real-life' application). This part of the system, which we refer to as RfaH-CTD, undergoes a dramatic conformational transformation from β-barrel to α-helical, which is stabilized by the N-terminal domain of the RfaH virulence factor (see Fig. masterclass-21-7-RfaH-CTD-fig).
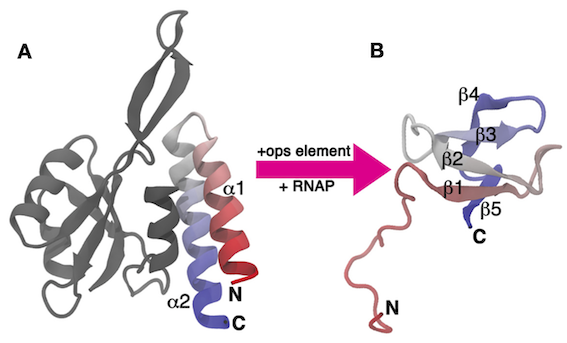
RfaH-CTD is simulated using a simplified, structure-based potential, called SMOG. The SMOG energy function has been designed to have two local minima corresponding to the β-barrel and α-helical states of RfaH-CTD. To achieve this goal, the SMOG energy function promotes native contacts, i.e. interactions that are present in the native structure(s). When using structure-based force fields, a function of the coordinates that is correlated with the energy of the system, such as the total number of native contacts, has been shown to be a good CV for enhanced-sampling simulations. Unfortunately, these types of CVs often involve a large number of atoms and are therefore computationally expensive to calculate at every step of the simulation. In this exercise, we will learn how to write and optimize these types of CVs.
In the data/exercise2 folder of the GitHub repository of this Masterclass, you will find:
stateA.pdb) and α-helical (stateB.pdb) states;topol.tpr file, which is needed to perform a MD simulation of this system with GROMACS;plumed.dat) to perform a metadynamics simulation using the total number of native contacts as CV. These contacts are defined using only the β-barrel conformation, which is the most populated state in the conditions we are simulating.The provided PLUMED input file looks as follows:

# reconstruct molecule WHOLEMOLECULESENTITY0=1-330 # CA-RMSDs from the two reference conformations # useful for monitoring the distance from the two metastable states rmsd_A: RMSDthe atoms that make up a molecule that you wish to align.REFERENCE=stateA.pdbcompulsory keyword a file in pdb format containing the reference structure and the atoms involved in the CV.TYPE=OPTIMALcompulsory keyword ( default=SIMPLE ) the manner in which RMSD alignment is performed.NOPBCrmsd_B: RMSD( default=off ) ignore the periodic boundary conditions when calculating distancesREFERENCE=stateB.pdbcompulsory keyword a file in pdb format containing the reference structure and the atoms involved in the CV.TYPE=OPTIMALcompulsory keyword ( default=SIMPLE ) the manner in which RMSD alignment is performed.NOPBC# list of 379 distances between atoms that are closer # than 0.6 nm in the reference PDB file (stateA.pdb, β-barrel state) d1: DISTANCE( default=off ) ignore the periodic boundary conditions when calculating distancesATOMS=1,110the pair of atom that we are calculating the distance between.NOPBCd2: DISTANCE( default=off ) ignore the periodic boundary conditions when calculating distancesATOMS=1,115the pair of atom that we are calculating the distance between.NOPBC# __FILL__ d379: DISTANCE( default=off ) ignore the periodic boundary conditions when calculating distancesATOMS=239,265the pair of atom that we are calculating the distance between.NOPBC# list of 379 switching functions to define a contact from the distance between two atoms c1: CUSTOM( default=off ) ignore the periodic boundary conditions when calculating distancesFUNC=1-erf(x^4)compulsory keyword the function you wish to evaluateARG=d1the input for this action is the scalar output from one or more other actions.PERIODIC=NO c2: CUSTOMcompulsory keyword if the output of your function is periodic then you should specify the periodicity of the function.FUNC=1-erf(x^4)compulsory keyword the function you wish to evaluateARG=d2the input for this action is the scalar output from one or more other actions.PERIODIC=NO # __FILL__ c379: CUSTOMcompulsory keyword if the output of your function is periodic then you should specify the periodicity of the function.FUNC=1-erf(x^4)compulsory keyword the function you wish to evaluateARG=d379the input for this action is the scalar output from one or more other actions.PERIODIC=NO # sum of switching functions = total number of contacts cv: COMBINEcompulsory keyword if the output of your function is periodic then you should specify the periodicity of the function.ARG=c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12,c13,c14,c15,c16,c17,c18,c19,c20,c21,c22,c23,c24,c25,c26,c27,c28,c29,c30,c31,c32,c33,c34,c35,c36,c37,c38,c39,c40,c41,c42,c43,c44,c45,c46,c47,c48,c49,c50,c51,c52,c53,c54,c55,c56,c57,c58,c59,c60,c61,c62,c63,c64,c65,c66,c67,c68,c69,c70,c71,c72,c73,c74,c75,c76,c77,c78,c79,c80,c81,c82,c83,c84,c85,c86,c87,c88,c89,c90,c91,c92,c93,c94,c95,c96,c97,c98,c99,c100,c101,c102,c103,c104,c105,c106,c107,c108,c109,c110,c111,c112,c113,c114,c115,c116,c117,c118,c119,c120,c121,c122,c123,c124,c125,c126,c127,c128,c129,c130,c131,c132,c133,c134,c135,c136,c137,c138,c139,c140,c141,c142,c143,c144,c145,c146,c147,c148,c149,c150,c151,c152,c153,c154,c155,c156,c157,c158,c159,c160,c161,c162,c163,c164,c165,c166,c167,c168,c169,c170,c171,c172,c173,c174,c175,c176,c177,c178,c179,c180,c181,c182,c183,c184,c185,c186,c187,c188,c189,c190,c191,c192,c193,c194,c195,c196,c197,c198,c199,c200,c201,c202,c203,c204,c205,c206,c207,c208,c209,c210,c211,c212,c213,c214,c215,c216,c217,c218,c219,c220,c221,c222,c223,c224,c225,c226,c227,c228,c229,c230,c231,c232,c233,c234,c235,c236,c237,c238,c239,c240,c241,c242,c243,c244,c245,c246,c247,c248,c249,c250,c251,c252,c253,c254,c255,c256,c257,c258,c259,c260,c261,c262,c263,c264,c265,c266,c267,c268,c269,c270,c271,c272,c273,c274,c275,c276,c277,c278,c279,c280,c281,c282,c283,c284,c285,c286,c287,c288,c289,c290,c291,c292,c293,c294,c295,c296,c297,c298,c299,c300,c301,c302,c303,c304,c305,c306,c307,c308,c309,c310,c311,c312,c313,c314,c315,c316,c317,c318,c319,c320,c321,c322,c323,c324,c325,c326,c327,c328,c329,c330,c331,c332,c333,c334,c335,c336,c337,c338,c339,c340,c341,c342,c343,c344,c345,c346,c347,c348,c349,c350,c351,c352,c353,c354,c355,c356,c357,c358,c359,c360,c361,c362,c363,c364,c365,c366,c367,c368,c369,c370,c371,c372,c373,c374,c375,c376,c377,c378,c379the input for this action is the scalar output from one or more other actions.PERIODIC=NO # metadynamics using "cv" metad: METADcompulsory keyword if the output of your function is periodic then you should specify the periodicity of the function.ARG=cv # Deposit a Gaussian every 500 time steps, with initial height # equal to 1.2 kJ/mol and bias factor equal to 60the input for this action is the scalar output from one or more other actions.PACE=500compulsory keyword the frequency for hill additionHEIGHT=1.2the heights of the Gaussian hills.BIASFACTOR=60 # Gaussian width (sigma) based on the CV fluctuations in unbiased runuse well tempered metadynamics and use this bias factor.SIGMA=10.0 # Gaussians will be written to filecompulsory keyword the widths of the Gaussian hillsFILE=HILLS ... # print useful stuff PRINTcompulsory keyword ( default=HILLS ) a file in which the list of added hills is storedARG=cv,rmsd_A,rmsd_B,metad.biasthe input for this action is the scalar output from one or more other actions.STRIDE=500compulsory keyword ( default=1 ) the frequency with which the quantities of interest should be outputFILE=COLVARthe name of the file on which to output these quantities
The objectives of this exercise are to:
Suggestions:
STRIDE option on the METAD line.Please keep in mind that:
gmx mdrun -plumed plumed.dat -ntomp 4 -noddcheck. You can adjust the number of CPU cores you want to use (here 4, OpenMP parallelization), based on the available resources. The system is not particularly big, therefore using a large number of cores might be inefficient.